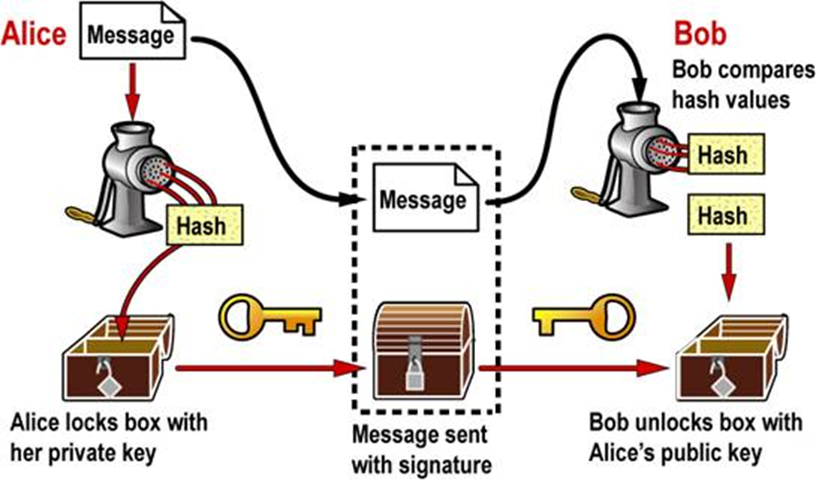
不安全的实例

写在前面

卧村密码学报郭福春老师更新了一些针对签名的攻击方案demo，感觉很适合反复学习背诵全文（常见的密码方案攻击方法，加强挑刺能力hhh）pdf链接：documents.uow.edu.au/~fuchun/jow/052.pdf下面是对pdf中例子的总结，如有疑问还请读者多指教~

学习目标

第1步：提出有效但不安全的方案。

第2步：了解它们为什么不安全或知道如何攻击它们。

第3步：具有修复不安全性的能力。

第4步：可以在修复安全方案后证明它们的安全性。

Schemes

3.1 Scheme

Let $(\mathbb{G},g,p)$ be the cyclic group and $H:{0,1}^{*}\to\mathbb{Z}_{p}$ be the cryptographic hash function that will be shared by all users.

KeyGen: The key generation algorithm chooses a random number $\alpha\in\mathbb{Z}{p}$ , computes $g{1}=g^{\alpha}$ , and returns a public/secret key pair $(p k,s k)$ as follows:

$p k=g_{1},s k=\alpha.$

给定循环群 $(G, g, p)$（$|G|=p$）和哈希函数 $H:{0,1}^* \to Z_p$ 。密钥生成选择随机私钥 $\alpha \in Z_p$，计算公钥元素 $g_1 = g^\alpha$。输出公钥 $pk = g_1$，私钥 $sk = \alpha$。

Sign: The signing algorithm takes as input a message $m\in{0,1}^{*}$ and the secret key $s k$ . It computes the signature $\sigma_{m}$ on $m$ as

$\sigma_{m}=\alpha+H(m)\mod p.$

对于消息 $m$，签名者直接计算 $\sigma_m = \alpha + H(m) \pmod p$。(注意：此方案签名不使用随机数)**。

Verify: The verification algorithm takes as input a message-signature pair $(m,\sigma_{m})$ and the public key $p k$ . It accepts the signature if

$g^{\sigma_{m}}=g_{1}\cdot g^{H(m)}.$

给定消息 $m$ 和签名 $\sigma_m$，验证者检查是否有 $g^{\sigma_m} \overset{?}{=} g_1 \cdot g^{H(m)}$ 。若等式成立则接受签名，否则拒绝。

Question 1 Is this signature scheme secure against forgeability in the key-only attack?

仅公钥攻击（Key-Only Attack）： 安全。攻击者只有公钥 $g_1 = g^\alpha$。要伪造任意消息的有效签名，需要求解 $\alpha$ 使 $g_1 = g^\alpha$，这相当于离散对数问题，一般认为在循环群上难以解决。因此在仅有公钥的情况下，攻击者无法直接计算出合法签名，方案在该模型下是安全的。

Question 2 Is this signature scheme secure in the EUF-CMA security model?

存在性不可伪造-选择消息攻击（EUF-CMA）： 不安全。 在允许查询签名的情况下，攻击者可以一条签名查询就完全攻破方案。具体地，在EUF-CMA安全性游戏中，攻击者先选定一个消息 $m0$，查询其签名 $\sigma{m0} = \alpha + H(m_0)$。攻击者由此轻易解出私钥 $\alpha = \sigma{m0} - H(m_0)$（在模$p$下计算）。得到私钥后，攻击者可自行为任何消息 $m^*$计算签名 $\sigma{m^} = \alpha + H(m^)$，从而成功伪造。这种攻击利用了签名值直接暴露了私钥信息，违反了存在性不可伪造要求。因此本方案在 EUF-CMA 模型下显然不安全。

EUF-CMA
这一模型中的CMA指Chosen Message Attack，即选择消息攻击，本质上与CPA其实是一样的，只不过在数字签名等算法中，用消息一词要比明文更加贴切。CMA和CPA都是形容敌手能自由地向算法提交输入并获得的相应输出这一能力。

EUF则是指存在性不可伪造，即 Existential UnForgeability，指的是对于消息认证、数字签名等算法而言，当敌手通过查询获得了 $q$ 个签名后，他无法再获得第 $q + 1$ 个签名。这一Game的示意图如下所示。在查询阶段，敌手 $\mathcal{A}$ 可不断与一实现了签名Oracle的 $\mathcal{C}$ 交互，来获得所提交消息 $m$的签名 $\sigma$。在进行 $q$ 次交互后，敌手将输出一对 $(m^{}, \sigma^{} )$。这一Game的主要步骤为：

Game中拥有一具有多项式资源的敌手 $\mathcal{A}$ 和一个能自由调用签名算法oracle $E$ 的挑战者$\mathcal{C}$。

$\mathcal{C}$ 随机选取$\mathsf{sk} \stackrel{$}{\leftarrow} {0,1}^{n}$，作为签名算法的私钥

$\mathcal{A}$ 向 $\mathcal{C}$ 提交消息 $m$, $\mathcal{C}$ 得到 $m$ 对应的签名 $\sigma $

重复步骤 3 $q$ 次 (即敌手查询 $q$ 次不同消息的签名)

$\mathcal{A}$ 输出一对 $(m^{}, \sigma^{})$;

$\mathcal{C}$ 对 $\sigma^{*}$ 进行验证，并返回验证结果;

若最后敌手输出的 $m^{}$ 未曾被查询过，且 $\sigma^{}$ 能通过验证，就可认为敌手挑战成功。这一结果即为“签名的伪造”，此处敌手的优势可写为：
$\mathrm{Adv}_{S}^{\mathrm{EUF-CMA}}(\mathcal{A}) = \mathrm{Pr}[\mathcal{A}\ \mathrm{forges}\ (m^{*}, \sigma^{*})]$

总结

本方案实际上是一个不使用随机数的简单签名方案。与之类似的是BLS 签名方案（Boneh–Lynn–Shacham），BLS签名中，私钥也是离散对数$x$，公钥为$g^x$，但签名计算为 $\sigma = H(m)^x$（将消息哈希映射为群元素后再取幂）。BLS签名虽然同样无随机数，但伪造签名等价于求解 $H(m)^\alpha$ 的离散对数或计算 Diffie-Hellman 难题，在随机预言机模型下被证明满足 EUF-CMA 安全。而3.1方案仅将哈希值与私钥线性相加，签名直接泄露私钥，安全性显著弱于BLS等经典方案。

BLS signatures

3.2 Scheme

Let $(\mathbb{G},g,p)$ be the cyclic group and $H:{0,1}^{*}\to\mathbb{Z}_{p}$ be the cryptographic hash function that will be shared by all users.

KeyGen: The key generation algorithm chooses a random number $\alpha\in\mathbb{Z}{p}$ , computes $g{1}=g^{\alpha}$ , and returns a public/secret key pair $(p k,s k)$ as follows:

$p k=g_{1},s k=\alpha.$

同样取循环群 $(G, g, p)$和哈希函数 $H:{0,1}^* \to Z_p$。生成私钥 $\alpha \in Z_p$，计算 $g_1 = g^\alpha$，公钥 $pk = g_1$，私钥 $sk = \alpha$

Sign: The signing algorithm takes as input a message $m\in{0,1}^{*}$ and the secret key $s k$ .

• Choose a random $r\in\mathbb{Z}{p}$ and compute $\sigma{1}=g^{r}$ .
• Compute $\sigma{2}=r+\alpha H(m)$ mod $p$ .
• Return the signature $\sigma{m}=(\sigma{1},\sigma{2})$ .

Sign： 对消息 $m$，签名者执行： (1) 选取随机 $r \in Z_p$，计算 $\sigma_1 = g^r$； (2) 计算 $\sigma_2 = r + \alpha \cdot H(m) \pmod p$ ； (3) 输出签名 $\sigma_m = (\sigma_1, \sigma_2)$。

Verify: The verification algorithm takes as input a message-signature pair $(m,\sigma_{m})$ and the public key $p k$ . It accepts the signature if

$g^{\sigma_{2}}=\sigma_{1}\cdot g_{1}^{H(m)}.$

Verify： 验证者对签名 $(\sigma_1,\sigma_2)$检查：是否 $g^{\sigma_2} \overset{?}{=} \sigma_1 \cdot g_1^{\,H(m)}$。展开验证式可见，左边$g^{\sigma_2} = g^{r+\alpha H(m)}$，右边$\sigma_1 \cdot g_1^{H(m)} = g^r \cdot (g^\alpha)^{H(m)} = g^{r+\alpha H(m)}$，二者相等则签名有效。

Question 3 Is this signature scheme secure against forgeability in the key-only attack?

仅公钥攻击： 安全。 攻击者只有公钥 $g_1 = g^\alpha$ 和哈希函数。想要直接伪造，需要找到 $(\sigma_1,\sigma_2)$ 满足 $g^{\sigma_2} = \sigma_1 \cdot g_1^{H(m^)}$。这要求满足 $\sigma_2 = r + \alpha H(m^)$ 且 $\sigma_1 = g^r$，其中 $\alpha$未知。攻击者相当于需要同时猜出正确的 $r$ 和 $\alpha$ 才能通过验证。在离散对数难题困难的假设下，没有签名查询的情况下攻击者无法推导出$\alpha$或有效的$(r,\sigma_2)$组合，因此应视为在仅公钥场景下安全。

Question 4 Is this signature scheme secure in the EUF-CMA security model?

EUF-CMA 攻击： 不安全。 攻击者可以利用两条签名查询构造线性组合攻击来伪造新消息签名。设攻击者请求消息$m_1, m_2$的签名：

得到$\sigma{m_1}=(\sigma{1,1}=g^{r1},\,\sigma{2,1}=r_1+\alpha H(m_1))$；
和$\sigma{m_2}=(\sigma{1,2}=g^{r2},\,\sigma{2,2}=r_2+\alpha H(m_2))$。

攻击者选择欲伪造签名的目标消息$m^$，令其哈希值 $H(m^)$ 满足线性关系：$H(m^) = c_1 \cdot H(m_1) + c_2 \cdot H(m_2) \pmod p$，其中 $c_1, c_2 \in Z_p$ 可由攻击者自行选定（因为哈希值是在模$p$下的数，攻击者可以通过解方程选取合适的系数，若视$H$为随机预言，可随机尝试消息直至找到满足关系的$H(m^)$）。攻击者构造：

$\displaystyle \sigma^*1 = (\sigma{1,1})^{c1} \cdot (\sigma{1,2})^{c_2} = g^{c_1 r_1 + c_2 r_2}$，
$\displaystyle \sigma^*2 = c_1 \sigma{2,1} + c2 \sigma{2,2} \pmod p = c_1(r_1+\alpha H(m_1)) + c_2(r_2+\alpha H(m_2))$。

由于$H(m^) = c_1 H(m_1)+c_2 H(m_2)$，可展开验证：
左边$g^{\sigma^_2} = g^{c_1(r_1+\alpha H(m_1)) + c_2(r_2+\alpha H(m_2))} = g^{c_1 r_1 + c_2 r_2 + \alpha(c_1 H(m_1)+c_2 H(m_2))} = g^{c_1 r_1 + c_2 r_2 + \alpha H(m^)}$。
右边$\sigma^_1 \cdot g_1^{H(m^)} = g^{c_1 r_1 + c_2 r_2} \cdot (g^\alpha)^{H(m^)} = g^{c_1 r_1 + c_2 r_2 + \alpha H(m^)}$。
二者完全相等，说明$(\sigma^_1,\sigma^_2)$通过了消息$m^$的验证。因为攻击者不需要知道$\alpha$就成功伪造了签名，说明该方案在选择消息攻击下存在严重漏洞，不满足EUF-CMA安全性。这一攻击之所以可行，是因为签名验证公式对不同消息呈线性关系，可以被攻击者利用线性组合已有签名来生成新签名。

总结

本方案是典型的Schnorr签名方案不当修改。正确的 Schnorr 签名 使用 $H(R,m)$ 将随机承诺 $R=g^r$ 和消息一起哈希，使签名方程变为 $s = r + \alpha \cdot H(R,m)$。这样验证为 $g^s \overset{?}{=} R \cdot g_1^{H(R,m)}$，攻击者无法对不同签名进行线性组合，因为哈希将$R$绑定到了特定消息。Schnorr签名在随机预言机模型下被广泛认为是EUF-CMA安全的。而本方案的哈希$H(m)$缺少对随机承诺$\sigma_1$的依赖，导致多个签名间存在线性可组合性，被攻击者利用而伪造新签名。另外，ElGamal签名（及其DSA/ECDSA变种）与本方案结构类似，也采用随机数 $k$ 产生 $r=g^k$，但ElGamal签名的$\sigma_2$计算为 $k^{-1}(H(m) - \alpha \cdot \log_g r)$，非线性地结合了$\alpha$和$r$，确保安全性。本方案简单相加导致线性泄露，与经典安全签名方案相比漏洞明显。

Schnorr签名

ElGamal签名

密钥生成：

选取一个足够大的素数p（十进制位数不低于160），以便于在 $\cdot Z_{p}$ 上求解离散对数问题是困难的。

选取Z*的生成元g。

随机选取整数 $\mathsf{d},0\leq d\leq p-2$ ，并计算 $y^{d}\equiv y\bmod p$ 。

签名：A选取随机数k $\in Z_{p-1}$ ，并且 $g c d(k,p-1)=1$ ，对消息进行签名
$s i g_{d}(m,k)=(r,s)$
其中 $r\equiv g^{k}\bmod p~,~s\equiv(m-d r)k^{-1}\bmod p-1~.$

验证：如果 $\boldsymbol{g}^{m}\equiv\boldsymbol{y}^{r}\boldsymbol{r}^{s}$ mod $p$ ，那么验证成功，否则验证失败。这里验证成功的原理如下，首先我们有 $y^{r}r^{s}\equiv g^{d r}g^{k s}\equiv g^{d r+k s}$ ，又因为 $ s\equiv(m-d r)k^{-1}{\bmod{p}}-1 $，所以 $k s\equiv m-d r{\bmod{p}}-1$ ，进而 $k s+d r=a*(p-1)+m$ ，所以 $g^{k s+d r}=g^{a*(p-1)+m}=(g^{p-1})^{a}*g^{m}$ 。所以根据费马定理，可得：
$g^{k s+d r}\equiv g^{m}{\bmod{p}}$
ps： ElGamal常见攻击 ——完全破译攻击

攻击条件 ：

p太小或无大素因子
如果p太小我们可以直接用大部小步算法分解，或者如果其无大的素因子，我们可以采用PohlingHellman算法计算离散对数即可进而求出私钥。

随机数k复用
如果签名者复用了随机数k，那么攻击者就可以轻而易举地计算出私钥。具体的原理如下：假设目前有两个签名都是使用同一个随机数进行签名的。那么我们有
$\begin{array}{c}{r\equiv g^{k}\bmod p}\\ {s_{1}\equiv(m_{1}-d r){k^{-1}}\bmod p-1}\\ {r\equiv g^{k}\bmod p}\\ {s_{2}\equiv(m_{2}-d r){k^{-1}}\bmod p-1}\end{array}$
进而有
>$$ >\begin{array}{c}{{s_{1}k\equiv m_{1}-d r\bmod p-1}}\\ {{s_{2}k\equiv m_{2}-d r\bmod p-1}}\end{array} >$$ >

两式相减
$k(s_{1}-s_{2})\equiv m_{1}-m_{2}{\bmod{p}}-1$
这里， $s{1},s{2},m{1},m{2},p-1$ 均已知，所以我们可以很容易算出 $k{\circ}$ 当然，如果$g c d(s{1}-s_{2},p-1)!=1$ 的话，可能会存在多个解，这时我们只需要多试一试。进而，我们可以根据s的计算方法得到私钥d，如下
$d\equiv\frac{m-k s}{r}$

3.3 Scheme

Let $(\mathbb{G},g,p)$ be the cyclic group and $H:{0,1}^{*}\to\mathbb{Z}_{p}$ be the cryptographic hash function that will be shared by all users.

KeyGen: The key generation algorithm chooses random numbers $\alpha,\beta\in\mathbb{Z}{p}$ , computes $g{1}=g^{\alpha}$ , $g_{2}=g^{\beta}$ , and returns a public/secret key pair $(p k,s k)$ as follows:

$p k=(g_{1},g_{2}),s k=(\alpha,\beta).$

在循环群 $(G, g, p)$中取随机私钥 $\alpha,\beta \in Z_p$，计算 $g_1 = g^\alpha, g_2 = g^\beta$。公钥 $pk=(g_1,g_2)$，私钥 $sk=(\alpha,\beta)$。

Sign: The signing algorithm takes as input a message $m\in{0,1}^{*}$ and the secret key $s k$ . It computes the signature $\sigma_{m}$ on $m$ as

$\sigma_{m}=\alpha+H(m)\cdot\beta\mod p.$

对消息 $m$，计算签名值为单个整数：$\displaystyle \sigma_m = \alpha + \beta \cdot H(m) \pmod p$。(注：无随机数参与，签名为私钥线性组合)

Verify: The verification algorithm takes as input a message-signature pair $(m,\sigma_{m})$ and the public key $p k$ . It accepts the signature if

$g^{\sigma_{m}}=g_{1}\cdot g_{2}^{H(m)}.$

验证者检查：$g^{\sigma_m} \overset{?}{=} g_1 \cdot g_2^{\,H(m)}$。代入$\sigma_m$展开，右边$g_1 \cdot g_2^{H(m)} = g^\alpha \cdot (g^\beta)^{H(m)} = g^{\alpha + \beta H(m)}$，恰好等于左边$g^{\sigma_m}$，因此签名正确性成立。

Question 5 Is this signature scheme secure against forgeability in the key-only attack?

仅公钥攻击： 安全。 攻击者仅有公钥 $(g_1=g^\alpha, g_2=g^\beta)$。要直接伪造消息$m^$的签名$\sigma^=\alpha+\beta H(m^*)$，需要同时未知量$\alpha,\beta$的正确线性组合。这相当于从公钥中同时求出$\alpha,\beta$，属于计算Diffie-Hellman类似的困难问题（因为$g_1=g^\alpha, g_2=g^\beta$，已知这两个值单独求$\alpha,\beta$是离散对数难题，而同时求解更无捷径）。因此在无签名查询时，本方案应是不可伪造的。

Question 6 Is this signature scheme secure in the EUF-CMA security model?

EUF-CMA 攻击： 不安全。 攻击者通过两条签名查询即可解出私钥，从而伪造任意签名。具体来说，攻击者请求消息$m_1, m_2$的签名：

$\sigma_{m_1} = \alpha + \beta H(m_1)$
$\sigma_{m_2} = \alpha + \beta H(m_2)$

视这两式为关于未知数$\alpha,\beta$的线性方程组。因为$H(m_1),H(m_2)$已知，攻击者从中可立即解出：

$\beta = \frac{\sigma_{m_1} - \sigma_{m_2}}{\,H(m_1) - H(m_2)\,} \pmod p,$ $\alpha = \sigma_{m_1} - \beta H(m_1) \pmod p.$

由此攻击者获得了完整私钥$(\alpha,\beta)$。剩下的游戏就简单了：攻击者可以用求得的$\alpha,\beta$为任何消息$m^$计算$\sigma^=\alpha + \beta H(m^)$，从而成功伪造签名。可见，本方案*在两次签名查询后即被完全攻破，不满足EUF-CMA安全性。

总结

本方案使用了两个独立私钥的线性组合来签名，但缺乏随机盐值随机化。与之形成对比的是 Okamoto 签名方案（亦称双重秘密 Schnorr 签名）。Okamoto签名中公钥为$(g_1^{\alpha}g_2^{\beta})$，签名者使用两个私钥并为每次签名选择两个随机数，产生二维的承诺值，再通过挑战哈希分别绑定这两个随机承诺，得到两个响应。这等价于对$\alpha,\beta$引入随机线性组合，避免了简单的线性泄露，从而是安全的。而本方案中没有任何随机化，导致不同签名之间私钥的线性组合固定不变，攻击者只需两条查询即可解方程求得秘密。另一经典方案 DSA 也可以看作是两部分（$r,s$）构成，其中$s$同时包含私钥和消息哈希，但因为有随机$k$的乘法逆模运算，方程并非简单可解。本方案的构造过于简单，安全性远不如上述经典方案。

Okamoto 签名方案:

选择一个大素数 $p$ 和一个素数 $q$，使得 $q$ 整除 $p-1$，选择两个生成元 $g_1, g_2$ 属于 $\mathbb{Z}_p^$，其阶均为 $q$，选择一个哈希函数 $H: {0, 1}^ \to \mathbb{Z}_q$。

密钥生成：

签名者选择两个随机整数作为私钥：$x_1, x_2 \in \mathbb{Z}_q$。

计算对应的公钥组件：$y_1 = g_1^{x_1} \pmod{p}$，$y_2 = g_2^{x_2} \pmod{p}$。

计算最终的公钥：$y = y_1 y_2 = g_1^{x_1} g_2^{x_2} \pmod{p}$。

私钥为 $(x_1, x_2)$。

公钥为 $(p, q, g_1, g_2, y)$。

签名：对于消息 $M$

签名者选择两个随机整数：$k_1, k_2 \in \mathbb{Z}_q$。

计算承诺值 (commitment): $r = g_1^{k_1} g_2^{k_2} \pmod{p}$。

计算挑战值 (challenge): $e = H(M || r)$，其中 $||$ 表示串联。

计算响应值 (response):

$s_1 = (k_1 + e x_1) \pmod{q}$

$s_2 = (k_2 + e x_2) \pmod{q}$

签名为 $(r, s_1, s_2)$。

验证：验证签名 $(r, s_1, s_2)$ 对消息 $M$:

验证者接收到消息 $M$ 和签名 $(r, s_1, s_2)$ 以及签名者的公钥 $(p, q, g_1, g_2, y)$。

计算挑战值：$e = H(M || r)$。

计算验证值：$v = g_1^{s_1} g_2^{s_2} y^{-e} \pmod{p}$。

如果 $v = r \pmod{p}$，则签名有效，否则无效。如果签名是有效生成的，那么：
$v = g_1^{s_1} g_2^{s_2} y^{-e} \pmod{p}$
$v = g_1^{k_1 + e x_1} g_2^{k_2 + e x_2} (g_1^{x_1} g_2^{x_2})^{-e} \pmod{p}$
$v = g_1^{k_1} g_1^{e x_1} g_2^{k_2} g_2^{e x_2} g_1^{-e x_1} g_2^{-e x_2} \pmod{p}$
$v = g_1^{k_1} g_2^{k_2} \pmod{p}$
$v = r \pmod{p}$

数字签名算法（DSA）：选择一个大素数 $p$ (通常为 1024, 2048 或 3072 位)。选择一个素数 $q$ (通常为 160, 224 或 256 位)，使得 $q$ 整除 $p-1$。选择一个生成元 $g \in \mathbb{Z}_p^*$，其阶为 $q$。$g$ 的计算方法通常是选取任意 $h \in {2, \dots, p-2}$ 并计算 $g = h^{(p-1)/q} \pmod{p}$，直到 $g > 1$。选择一个加密哈希函数 $H$ (例如 SHA-1, SHA-256 等)，其输出长度与 $q$ 的长度相匹配。

密钥生成：

签名者选择一个随机整数作为私钥：$x \in {1, \dots, q-1}$。

计算对应的公钥：$y = g^x \pmod{p}$。

私钥为 $x$。

公钥为 $(p, q, g, y)$。

签名：对于消息 $M$

签名者选择一个随机整数作为每条消息的临时私钥 (或称 nonce): $k \in {1, \dots, q-1}$。此 $k$ 值必须对每条签名唯一且保密。

计算 $r = (g^k \pmod{p}) \pmod{q}$。如果 $r=0$，则重新选择 $k$。

计算消息的哈希值：$h = H(M)$。将哈希值转换为一个小于 $q$ 的整数 (通常取哈希值的最左边 $q$ 比特)。

计算 $s = (k^{-1} (h + x r)) \pmod{q}$。这里的 $k^{-1}$ 是 $k$ 对 $q$ 的模逆。如果 $s=0$，则重新选择 $k$。

签名为 $(r, s)$。

验证：对于签名 $(r, s)$ 和消息 $M$:

验证者接收到消息 $M$ 和签名 $(r, s)$ 以及签名者的公钥 $(p, q, g, y)$。

检查是否 $1 \le r < q$ 且 $1 \le s < q$。如果不是，则签名无效。

计算消息的哈希值：$h = H(M)$。将哈希值转换为一个小于 $q$ 的整数。

计算 $w = s^{-1} \pmod{q}$。这里的 $s^{-1}$ 是 $s$ 对 $q$ 的模逆。

计算 $u_1 = (h w) \pmod{q}$。

计算 $u_2 = (r w) \pmod{q}$。

计算验证值：$v = ((g^{u_1} y^{u_2}) \pmod{p}) \pmod{q}$。

如果 $v = r$，则签名有效，否则无效。如果签名是有效生成的，那么：

$s = (k^{-1} (h + x r)) \pmod{q}$
$ks \equiv h + xr \pmod{q}$
$h \equiv ks - xr \pmod{q}$
$h w \equiv ksw - xrw \pmod{q}$
由于 $w = s^{-1} \pmod{q}$，$sw \equiv 1 \pmod{q}$。
$u_1 \equiv k - xr w \pmod{q}$
$u_1 \equiv k - x u_2 \pmod{q}$
根据指数的模运算性质：
$g^{u_1} y^{u_2} \equiv g^{k - x u_2} y^{u_2} \pmod{p}$
$g^{u_1} y^{u_2} \equiv g^k g^{-x u_2} (g^x)^{u_2} \pmod{p}$
$g^{u_1} y^{u_2} \equiv g^k g^{-x u_2} g^{x u_2} \pmod{p}$
$g^{u_1} y^{u_2} \equiv g^k \pmod{p}$
所以，$v = (g^{u_1} y^{u_2} \pmod{p}) \pmod{q} = (g^k \pmod{p}) \pmod{q} = r$。

3.4 Scheme

Let $(\mathbb{G},g,p)$ be the cyclic group and $H:{0,1}^{*}\to\mathbb{Z}_{p}$ be the cryptographic hash function that will be shared by all users.

$p k=(g_{1},g_{2}),s k=(\alpha,\beta).$

在循环群 $(G, g, p)$中，选取私钥 $\alpha,\beta \in Z_p$，计算 $g_1 = g^\alpha, g_2 = g^\beta$，输出公钥 $pk=(g_1,g_2)$，私钥 $sk=(\alpha,\beta)$ 。

Sign: The signing algorithm takes as input a message $m\in{0,1}^{*}$ and the secret key $s k$ .

Choose a random $r\in\mathbb{Z}{p}$ and compute $\sigma{1}=g^{r}$ .
Compute $\sigma_2 = \frac{\alpha + r}{\,\beta + H(m)\,} \pmod p$.
Return the signature $\sigma{m}=(\sigma{1},\sigma_{2})$ .

对消息 $m$： (1) 选择随机数 $r \in Z_p$，计算 $\sigma_1 = g^r$； (2) 计算 $\sigma_2 = \frac{\alpha + r}{\,\beta + H(m)\,} \pmod p$ ；(3) 输出签名 $\sigma_m = (\sigma_1,\sigma_2)$。 （注：上述 $\sigma_2$ 公式根据原文推导得到，应为将$\alpha+r$乘以$(\beta+H(m))^{-1}$取模$p$ 。）

Verify: The verification algorithm takes as input a message-signature pair $(m,\sigma_{m})$ and the public key $p k$ . It accepts the signature if

$\Bigl(g_{2}g^{H(m)}\Bigr)^{\sigma_{2}}=g_{1}\cdot\sigma_{1}.$

验证者计算校验：$(g_2 \cdot g^{H(m)})^{\sigma_2} \overset{?}{=} g_1 \cdot \sigma_1$ 。将$\sigma_2$代入左侧，得到：

$\big(g^\beta \cdot g^{H(m)}\big)^{\sigma_2} = g^{(\beta + H(m))\sigma_2} \stackrel{!}{=} g_1 \cdot \sigma_1 = g^\alpha \cdot g^r = g^{\alpha+r}.$

由于签名者构造$\sigma_2$时满足$(\beta+H(m))\sigma_2 = \alpha+r$，因此验证等式成立，签名有效。

Question 7 Is this signature scheme secure against forgeability in the key-only attack?

仅公钥攻击： 如果不伪造$(\sigma_1,\sigma_2)$：安全。 攻击者仅知公钥 $g_1=g^\alpha, g_2=g^\beta$。想要直接伪造，需要找到$(\sigma_1,\sigma_2)$使得 $(g_2 g^{H(m^)})^{\sigma_2} = g_1 \cdot \sigma_1$。这要求$(\beta + H(m^))\sigma_2 = \alpha + r$ 且 $\sigma_1=g^r$ 同时成立，相当复杂。攻击者即使猜测$r$，仍需满足 $\sigma_2 = (\alpha+r)/(\beta+H(m^))$，但$\alpha,\beta$未知难以满足。此外，$\sigma_1=g^r$提供了一定的*随机遮蔽，进一步增加了直接伪造的难度。因此在无签名查询时，本方案应无法直接伪造。

如果伪造$(\sigma_1,\sigma_2)$：不安全。 给定公钥 $(g_1,g_2)$ 与消息 $m$，攻击者可执行：

取随机 $\sigma_2\stackrel{$}{\leftarrow}\mathbb Z_p$。
计算 $\sigma_1 \;=\;(g_2\cdot g^{H(m)})^{\sigma_2}\cdot g_1^{-1}.$ 该幂与乘法均在公开群中完成，无须离散对数。
输出 $\sigma=(\sigma_1,\sigma_2)$。

验证方程立刻成立： $g_2g^{H(m)})^{\sigma_2}=g_1\sigma_1$
因为右端就是左端乘以 $g_1^{-1}\,g_1$。攻击者完全不需要私钥 $(\alpha,\beta)$ 或随机值 $r$。GeeksforGeeks cs.purdue.edu

类似伪造：

课本 RSA 签名：任选 $s\leftarrow\mathbb Z_n^{!*}$，设 $m=s^e\bmod n$，则 $(m,s)$ 为有效签名——与上式同样“先选 σ₂，再配 σ₁”。Cryptography Stack Exchange
原版 ElGamal 签名（无哈希）：可取 $e,v$ 两参数伪造 $(r,s)$ 使验证等式成立。Wikipedia

这些例子都说明：若验证等式呈现出“可任意选未知数、再解另一个未知数”的结构，往往会导致 KOA 伪造。

Question 8 Is this signature scheme secure in the EUF-CMA security model?

EUF-CMA 攻击： 不安全。 攻击者可以通过多次签名查询逐步求解出私钥或构造等式来伪造签名。虽然比起3.3方案，本方案在签名中加入了随机数$r$，但仍存在线性关系可被利用：每个签名满足 $(\beta+H(m))\sigma_2 - r = \alpha$（等价于$(\beta+H(m))\sigma_2 = \alpha + r$）。不同消息的签名提供了多条这样的等式：

$(\beta+H(m_1))\sigma_{2,1} - r_1 = \alpha,$ $(\beta+H(m_2))\sigma_{2,2} - r_2 = \alpha.$

攻击者知道$\sigma{2,1},\sigma{2,2},H(m1),H(m_2)$以及$\sigma{1,1}=g^{r1}, \sigma{1,2}=g^{r_2}$。虽然单独未知$r_1,r_2$，但两式右侧同为$\alpha$，攻击者可消去$\alpha$得到：

$(\beta+H(m_1))\sigma_{2,1} - (\beta+H(m_2))\sigma_{2,2} = r_1 - r_2.$

右边$r1-r_2 = \log_g(\sigma{1,1}/\sigma_{1,2})$，攻击者若能计算离散对数就可解出一个关于$\beta$的线性方程。然而离散对数计算困难，因此需要更多查询累积信息。不过，由于攻击者可以选择消息，多次查询可形成多元线性方程组求解$\alpha,\beta$。一旦取得足够多的签名（例如通过选取不同$H(m)$值形成线性独立方程），攻击者即可解出私钥 $\alpha,\beta$，进而伪造任意签名。因此，本方案并未通过单一随机数完全阻止线性攻击，在EUF-CMA下仍不安全。

总结

本方案可看作是对双秘密密钥签名的一次尝试改进，引入了随机数和分母$(\beta+H(m))$以提高安全性，但效果不佳。经典的 Okamoto签名方案 提供了一种安全构造思路：它使用两个随机数分别对应两个私钥部分，并采用哈希挑战将随机承诺与消息绑定，从而生成两个响应。Okamoto签名的验证涉及同时检验两部分方程，保证了安全性。而3.4方案仅用一个随机数尝试掩饰两个私钥的组合，其验证等式仍然是一元的线性关系，安全性不足。可以说，3.4方案是一个未充分随机化的双秘钥签名，对比Okamoto等安全方案，它缺少足够的独立随机度，因而被攻击者利用签名间关系破解。

3.5 Scheme

Let $(\mathbb{G},g,p)$ be the cyclic group and $H:{0,1}^{*}\to\mathbb{Z}_{p}$ be the cryptographic hash function that will be shared by all users.

KeyGen: The key generation algorithm chooses a random number $\alpha\in\mathbb{Z}{p}$ , computes $g{1}=g^{\alpha}$ , and returns a public/secret key pair $(p k,s k)$ as follows:

$p k=g_{1},s k=\alpha.$

在循环群 $(G, g, p)$下，选择私钥 $\alpha \in Z_p$，计算公钥 $g_1 = g^\alpha$，输出 $pk = g_1$，$sk = \alpha$ 。

Sign: The signing algorithm takes as input a message $m\in{0,1}^{*}$ and the secret key $s k$ .

Choose random $r{1},r{2},t\in\mathbb{Z}{p}$ and compute $\sigma{1}=g^{r{1}},\sigma{2}=g^{r{2}},\sigma{3}=g^{t}.$ .
Compute $\displaystyle \sigma_4 = (r_1 \cdot H(m, pk, 1) + r_2 \cdot H(m, pk, 2)) / (\alpha + t \cdot H(\sigma_3)) \pmod p$
Return the signature $\sigma{m}=(\sigma{1},\sigma{2},\sigma{3},\sigma_{4})$ .

对消息 $m$ 和公钥 $pk$，签名者执行以下步骤：

选择随机 $r_1, r_2, t \in Z_p$，计算 $\sigma_1 = g^{r_1},\; \sigma_2 = g^{r_2},\; \sigma_3 = g^t$ 。
计算 $\displaystyle \sigma_4 = (r_1 \cdot H(m, pk, 1) + r_2 \cdot H(m, pk, 2)) / (\alpha + t \cdot H(\sigma_3)) \pmod p$ 。
输出签名 $\sigma_m = (\sigma_1,\; \sigma_2,\; \sigma_3,\; \sigma_4)$。

Verify: The verification algorithm takes as input a message-signature pair $(m,\sigma_{m})$ and the public key $p k$ . It accepts the signature if

$\sigma_{1}^{H(m,p k,1)}\cdot\sigma_{2}^{H(m,p k,2)}=(g_{1}\sigma_{3}^{H(\sigma_{3})})^{\sigma_{4}}.$

验证者给定 $(m, \sigma_m)$ 和公钥，计算并验证： $\sigma_1^{\,H(m,pk,1)} \cdot \sigma_2^{\,H(m,pk,2)} \ \overset{?}{=} \ \Big(g_1 \cdot \sigma_3^{\,H(\sigma_3)}\Big)^{\sigma_4}.$

Question 9 Is this signature scheme secure against forgeability in the key-only attack?

仅公钥攻击： 不安全。 在只知道 $pk = g1 = g^α$ 的情况下，为任意消息 $m$ 计算签名 $σ=(σ1,σ2,σ3,σ4)$，使得下列等式成立：

$\sigma_1^{H(m,pk,1)}\;\sigma_2^{H(m,pk,2)}=\bigl(g_1\,\sigma_3^{H(\sigma_3)}\bigr)^{\sigma_4}\,.$

置 $σ1 = 1_G$, $σ2 = 1_G$（群单位）。
随意选 $t←ℤ_p$，令 $σ3 = g^t$。
置 $σ4 = 0$。
- (1) 右端变为单位元，因为任何元素的 0 次幂皆为 1_G。
- 左端同样是单位元，因为 $σ1 = σ2 = 1_G$。
(1) 恒成立，不依赖 $α$ 或 $m*$。

无需私钥、无需调用 Sign 算法；整个过程对消息 $m^{\star} $完全独立，因此可对任意消息重用。 eitca.org Packetlabs
这种“零指数”手法在早期教材方案中屡见不鲜，被称作zero‑exponent forgery。 csrc.nist.gov crypto.stanford.edu

方案	是否抗 key‑only	关键机制
Scheme 3.5	✖ 易被零指数伪造	$\sigma_4$ 可令 0，并且 $\sigma_1,\sigma_2$可取单位元
Schnorr 签名	✔ EUF‑CMA 证明	将挑战 (e=H(m,R)) 固定进指数，禁止 0 指数 Cryptography Stack Exchange
紧致 DL‑基签名 (e.g., Boneh–Boyen)	✔ EUF‑KOA 起步	将消息、随机数和私钥紧耦合，避免独立调节 ScienceDirect

这些安全方案都会把随机挑战、消息与私钥耦合进同一指数，从而杜绝“幂 = 0”这类捷径。设计安全签名的经验法则：

禁止零指数——将哈希挑战嵌入指数且强制非零；
绑定消息与随机数——让验证式每一项都依赖 (H(m,\dots))；

Question 10 Is this signature scheme secure in the EUF-CMA security model?

EUF-CMA 攻击： 不安全。

总结

攻击者在零交互、零计算量的情况下即可输出合法签名，显然破坏了存在性不可伪造性‑仅公钥攻击 (EUF‑KOA) 的最低要求。