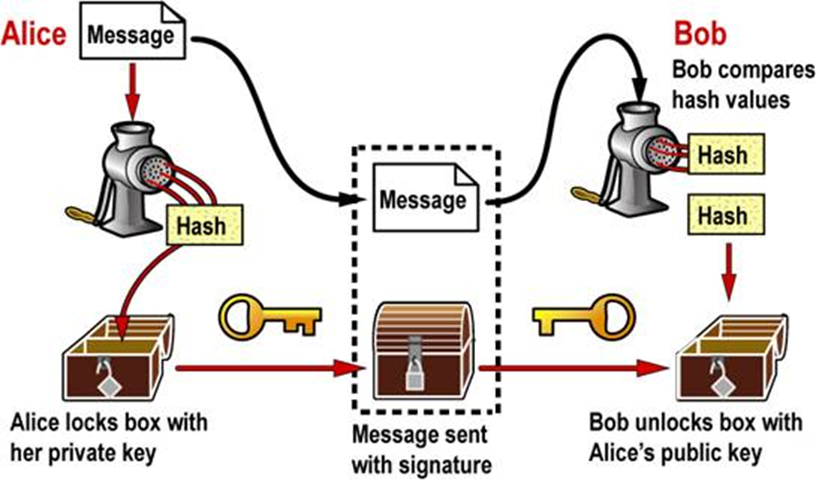
安全规约第四讲——安全规约入门
计算复杂性的规约理论
大致框架如下:
- 关于不可能:源于p和np问题是否等价未证明
- 计算问题里的表达方式和安全问题里的表达方式是相反的
- 一般表达的时候描述为a比b简单

- 解决b可以转化成解决a(a比b简单,故可通过解决b转化为解决a)
规约的描述是从较难到更难的过程,所谓规约就是证明我们关心的方案不比已有的方案简单,即研究一个问题困难度的下限
一些例子:
- 先输入problem A 的instence
- 想办法转化成b中的insetence
- 在将b的solution转化回a

- proof的重点:如何构造参数使得b可以转化为a
故有时候review证明者的思路可以尝试从后往前看
只可意会不可言传
例子2
例子3

- 随机选取w(ramdomly choose):只有这么设置,才能使得b中的instence space可以做到随机选取,具体原因和计算复杂性有关*。
密码中的安全规约

规约:problem->problem
安全规约:problem->scheme
安全规约的作用:解决一个困难问题要比攻破一个安全方案简单
注:安全规约和安全分析是不一样的,安全分析更多注重于已知的攻击算法,对于未公开的安全攻击方式无能为力,而安全规约则可以囊括一整个安全模型下的所有攻击方式,即使它没有公开。
证明策略

具体的框架&解释
首先做出一些定义
证明开始之前需要假设一个敌手
- 先模拟一个方案,设定允许询问什么&计算什么
- 如何提取出yp
- 分析解决困难问题p的优势是不可忽略的
Q:安全规约一定要分析嘛?
A:没有分析的安全规约一定不是完整的

安全规约更多的是证明a和b的关系,至于b是否存在不考虑
一些容易混淆的概念
real scheme VS simulated scheme
real scheme:通过运行算法得来的
simulated scheme:
challenger VS simulator
challenger:最好出现在安全模型里
simulator:最好出现在安全规约里
real attack VS simulation

- informations:敌手需要知道的信息,根据模型而来的
- 二者的区别可以粗暴的理解成两个平行世界的角色

有点类似于网络聊天中判队对方是人是狗
- 这里的规约算法只需模拟出敌手要的结果而已而不是整个算法,比如在证明cpa安全的时候我们无需把所有具体的算法都模拟出来
indistinguishable

如果不能判断b是通过哪种方法计算的,则称indistinguishable
注:这里的a要随机选取,否则可能会出现可区分行,比如如果a=1的概率超级高,则在选择方法的时候就可以对结果进行区分。
breaking to solution

可以通过三种方式转换

一二种比较常见
第三种比较特殊,是将一个判别式的规约问题转化为计算的规约问题

T=O(q):与询问次数有关,消不掉
q:与安全模型相关
tight reduction & Loose Reduction

- 目前所有的安全规约的方案都无法消除simulation time

- tight reduction:仍然比loose reduction好
- tight reduction会影响计算效率,如果一个方案需要考虑效率不要用这个
- 投偏应用的期刊(ieee)不要用tight reduction,会很别扭
lower bound security level

concrete security: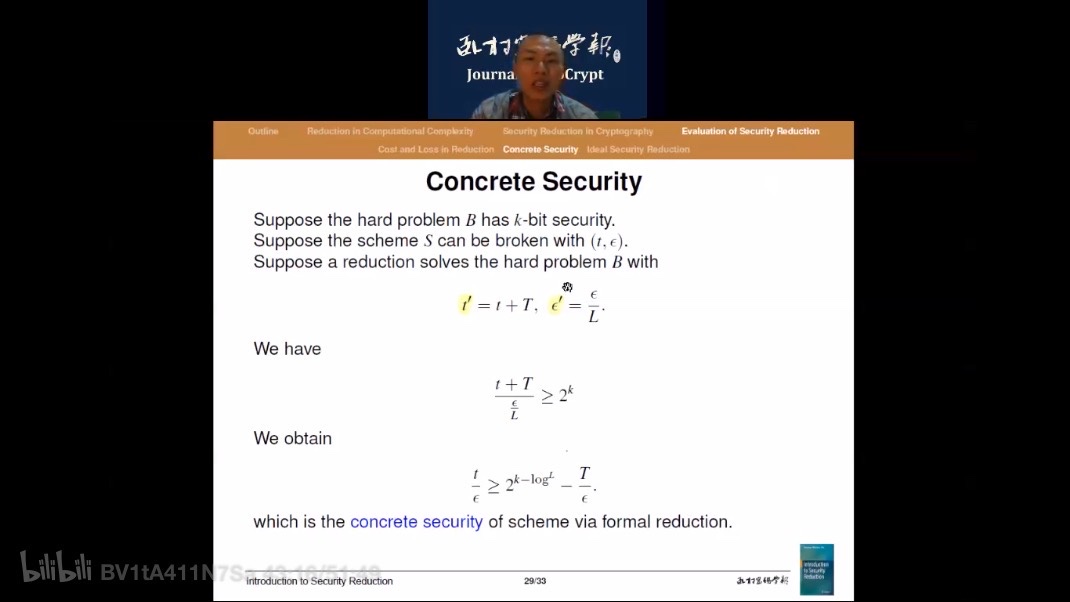

- l和t越小越好,似的右边的值无限接近2^k
完美的安全规约
需要满足以下四点:
但一般情况下这四点互斥,即无法达到多块好省。如下图:
- tradeoff:很神奇,覆盖了computer science
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Happy Shark!
评论