有限域

定义

有限域的运算

通过乘加来实现

除：u * v的逆元
减：u + v的逆元

举个例子

n为整数
q为素数
有限域中包含了q^n个元素。
有限域内每个元的长度都为n * |q|

素数域

群

阿贝尔群

定义：

用点号（而不用加或者乘），可以是有限域中的加号，乘号.etc

Ex：

可以通过H生成整个群的元素，所有的元素都可以通过h^i i=1,2,…得到

如何描述一个循环群？

G：群的空间
g：生成元
p：阶数

群元素

每个群元最少需要160bit

30期中有对安全等级做进一步解释

群中的简单问题和困难问题

有些计算必须要足够简单
有些计算必须要足够困难，例如公私钥（一个基本的困难问题是离散对数问题，并且只有某些构造的比较好的群才有离散对数这样的性质）

easy ：group exponentiation（群指数）

如上，定义一个运算，当x特别大的时候计算会比较困难，故采取先平方在乘的算法（square-and-multiply algorithm）

采用上述方法，最大只需要2^2n次运算即可

hard：Discrete Logarithm（离散对数）

如果G是一个具有素数阶的循环群，那么任意给定两个群元g h ，那么这个离散对数x必然存在，而且是唯一的，这就是为啥一般都比较喜欢具有素数阶的循环群。
如果可以很简单的解决离散对数问题，那么所有基于群对数的加密方案都会不安全。

以下介绍离散对数问题的计算复杂性：

Ω代表下界，指至少需要根号p

O代表上界

群的阶必须要大于160来抵抗特殊的攻击，如果小于则敌手最多只需2^80步即可攻破

群的选择

为什么要定义其他的一些更加复杂&高级的群而不直接使用有限域中已有的两个群？

有很多原因，比如椭圆曲线群，群元素可以用长度表示从而让其长度更短。

乘法群

q指大素数，p是比q小的一个素数
p只需要大于160bit，但q要大于1024bit（与RSA相似），因为目前存在一种特殊的攻击可以攻破该方案，使用这种攻击的前提就是q足够小

椭圆曲线群

主需要给出横坐标，从而减小其长度表示（y通过计算得出，故增加了计算量）
u·v：包含了有限域中的加法和乘法运算

基于椭圆曲线群的计算

基于以上算法，可以构造出更加复杂的方案，比如上图中的Question

双线性对

特点：将椭圆曲线上群的两个群元映射到一个乘法群上的群元，同时这种运算可以保持同态性。

同态性：最早由两位日本学者提出，他们想解决椭圆曲线上困难问题，故提出将定义在椭圆曲线上的问题映射到惩罚群上去，在乘法群内解决在反映射回来。

双线性对有3种：

Symmetric Pairing

定义

大小

实际上，80bit已经不够安全，现在最少需要128bit

Asymmetric Pairing 非对称对

定义

大小

因为目前有三种群 g1 g2 gt，为了确保安全，目前g1最少需要160bit，g2=gt最少需要1024bit，目的为了让g1群越小越好

pairing上的计算

在pairing上的计算可以拓展成乘法，指数，。。。，等其他方式的计算，实际上很多方案（比如加密，签名，认证等等）都是基于此扩展出来的，但是需要很高的技巧

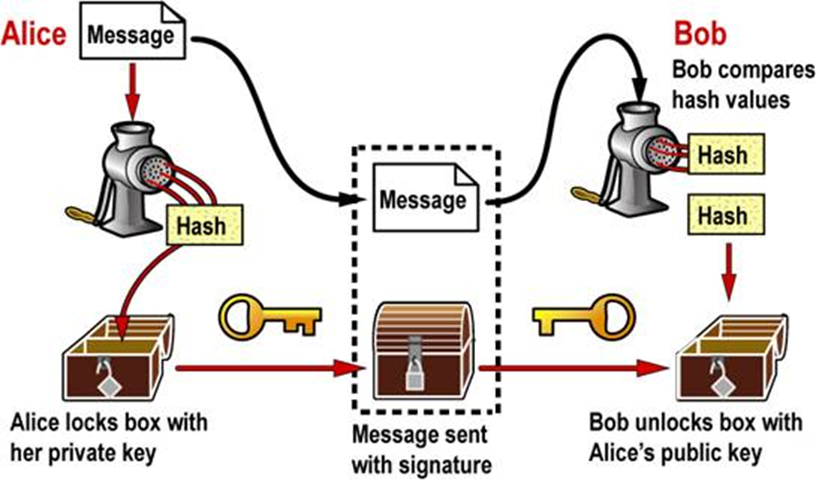
哈希函数 H(·)

其中的一个用途：缩短签名长度：如果有个签名方案是按每bit签名，若有个1g的文件不压缩的话就签到猴年马月了；相反通过hash缩小到一个定长长度在对hash签名就很快

基于安全性的分类

基于输出对哈希函数进行分类

可以分成三类：

n bit 的串：输出结果可以用作key，与对称密码结合用于加解密
Zp：
输出到群中：

为什么不直接用第二种取代第三种：如果使用第二种方法在方案构造中会出现不安全，只有用第三种才能构造出安全的方案。

随机函数

现有的公钥加密也是需要随机数得到，否则无法达到ind安全

现有的密码方案是依赖许多假设的

不安全的方案

错误的方案原因都类似的，下面以签名为例

不安全的数字前面

基础运算需要大量的去熟悉联系

第四个和第五个相似

6与1类似